Look closely at an International GCSE Mathematics examination and you’ll soon realise that answering the questions isn’t just about working with numbers, algebra, shapes, measures, and data.
In this blog article, Naomi Norman, independent education researcher, consultant, and co-author of the Pearson Edexcel International GCSE (9-1) Maths A Teaching Hub, looks at some of the less obvious requirements of exam questions. Drawing from the extensive guidance and support available in the Teaching Hub for every guided learning hour of the Mathematics course, Naomi offers suggestions on how to help students achieve the best possible results in the examination.
Students must understand the language of Mathematics
Mathematical terms have specific meanings that are crucial to giving accurate answers. Consider the word ‘reflex’, for example, in June 2023 Paper 2H question 7. This question asks students to ‘work out the size of reflex angle AOC’; and yet here’s the comment from the Examiners’ Report (available to download from the Exam Practice section of the Teaching Hub):
Question 7
… The reflex angle was labelled with angle notation to make it clear that this was the angle to find, but there were still a lot of answers between 90 and 180 degrees.
Mathematical vocabulary can also have nuances. For example, ‘estimating’ in everyday language means making a good guess, but in maths it can involve a specific procedure, such as ‘estimating the mean’ (see January 2023 Paper 1H, question 1, available on the Teaching Hub).
Additionally, different mathematical words can describe the same thing. For example, a price ‘decreased’, ‘reduced’, ‘deflated’ or ‘depreciated’ by 25% results in the same calculation (as explained in Teaching Hub Lesson 172: Revision Lesson 1: Percentages – see Teaching session 1).
What you can do
You may hope that exposing students to relevant mathematical vocabulary, the first time they meet a concept, is enough. However, this is unlikely to work for all students. Therefore, I suggest you:
- Introduce a word in the context of a relevant question and encourage students to write down its definition.
- Regularly revisit definitions. For example, whenever showing a geometric diagram (whatever the mathematical context), ask students to identify the reflex angles, the obtuse angles, the exterior angles, the isosceles triangle, the kite etc. Then ask how they identified them, encouraging the recall and vocalisation of definitions.
- Discuss synonyms for vocabulary. For example, whenever working on a percentage decrease question, ask students how the question could be re-written using a word different to ‘decrease’, but with the same meaning.
Students must be able to interpret commands
Understanding ‘command words’ – the instructions at the beginning of a question – is essential. Consider, for example, the first question of the January 2023 Paper 2H (available on the Teaching). This question begins ‘Show…’. Are your students aware that this indicates they must show all the working to get to a given answer? Then, question 4 asks students to ‘Work out…’, which means the examiner expects to see some working; and question 5a asks students to ‘Write down…’ implying no working at all is required.
Other command words indicate the ‘flow’ of answers. For example, June 2023 Paper 1H question 6d(i) begins ‘Factorise…’ (i.e. insert brackets by taking out common factors) and then question 6d(ii) begins ‘Hence…’. The word ‘hence’, provides the hint that part (ii) relates in some way to the answer to part (i); and yet the Examiners’ Report (available on Teaching Hub) states:
Question 6
… Quite a few students started again in part (ii), not understanding the meaning of ‘hence’.
Those students who started again unfortunately wasted precious exam time that they could have dedicated to answering other questions or double-checking answers.
What you can do
I suggest you:
- Frequently emphasize the command word that begins a question and discuss its meaning with students.
- Create a reference list on the classroom wall with explanations of common command words. For example:
| Command words | What you need to know |
| Show that | All working needed to get to a given answer. |
| Work out | Some working will be needed in order to get to an answer. |
| Write down | No working is needed. |
[Also see: ‘A Teacher’s Guide to Command Words‘]
Students must be familiar with common contexts
Many Mathematics questions involve everyday contexts. Typically, they fit into one of these nine categories:
- times – in activities like sports, walking, or travel
- money – in payments, such as for a car, or currency exchange
- weights – of food, animals, or parcels
- heights – of plants or buildings
- containers – for food (such as jars), liquids (such as vases), or items (such as boxes)
- games – involving spinners, counters or cards
- scores – in competitions, sports, tests, or quizzes
- weather – temperatures or rainfall
- genres – in books, in films, in clothing, colours
Of course, International GCSE Mathematics examiners work hard to select only contexts that are likely to be familiar to students, and which can be described using simple English. Nonetheless, it is worth dedicating a little time to ensuring students are comfortable with, at least, the contexts listed above. This will help students to avoid becoming distracted by descriptions relating to a question context, at the expense of what they need to do to demonstrate their mathematical competence.
What you can do
I suggest:
- When students are answering questions in context, ask them for words they can think of associated with that context. For example, if a question describes scores in a test, ask: ‘What other word could be used instead of ‘score’ in a maths question?’ (possible answers may be tally, mark, grade); ‘What activity, other than a test, might you be doing to achieve a score?’ Write down the words associated with different contexts. Then ask students to read the words aloud, to aid familiarity.
Students must be able to ‘read’ diagrams
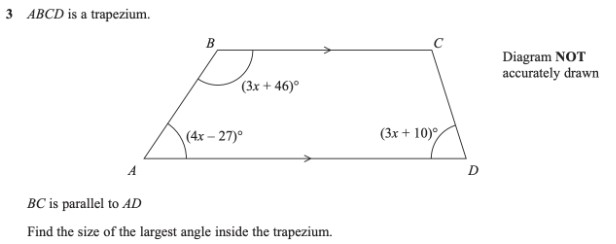
There are numerous types of mathematical diagrams that students may encounter in an International GCSE Mathematics exam. For example, consider this question with a diagram from June 2023 Paper 2H (available on the Teaching Hub):
When faced with questions like this, it is common for students to entirely focus on the text at the very beginning, and any text towards the end that tells them what they must ‘find’ or ‘work out’. Unfortunately, students often neglect to really look and notice what is in the middle – the features of the diagram! Comments from the Examiners’ Report suggest that this is exactly what happened for many students attempting to answer this question.
Question 3
Many students had difficulty with this question. Common errors included equating the opposite pair of angles, B and D, or summing base angles A and D to give 180°.
The examiner’s comment (also available on the Teaching Hub) suggests that students were focused on the initial textual information: ‘ABCD is a trapezium’ and the requirement at the end of the question to find an angle ‘inside the trapezium’. And so, they were seeking to make sense of the sum of angles in a trapezium. However, if students had spent time really looking at the diagram (in the middle), and noticed the parallel lines, students may have thought to use what they know regarding angles in parallel lines to answer the question.
As clearly stated by Roth (2002, p.20) in his research on graphs, diagrams do not ‘speak for themselves, but are read’1.
What you can do
I suggest you:
- Instruct students: ‘If a question includes a diagram, stop! Look carefully at the diagram and note its features’.
- Always give students a little time to simply look at a diagram in silence, before discussing observations.
- Make it a habit to regularly encourage students to ‘read’ diagrams. There are plenty of opportunities for such practice in Teaching Hub Lesson 179: Revision Lesson 8: Angles in Polygons.
A final word
Although mastering mathematical concepts is crucial, don’t forget to devote some time to the less obvious aspects of preparing students for their International GCSE Mathematics examinations. By addressing these, you can significantly boost your students’ chances of exam success.
Further reading
Find out more about International GCSE Teaching Hubs and take a free trial.
1 Roth, W. M. (2002). Reading graphs: Contributions to an integrative concept of literacy. Journal of Curriculum Studies, 34(1), 1–24. https://doi.org/10.1080/00220270110068885.
Sign up to receive our blog updates
Like what you read and want to receive more articles like this direct to your inbox? Subscribe to our blog and we’ll send you a fortnightly digest of the blog posts you may have missed, plus links to free resources to support your teaching and learning.