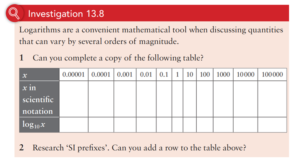
As Paula explored in her previous blog post in this series, research clearly identifies a concept-based, challenging, inquiry approach as necessary for deep understanding, an enjoyment of mathematics and improved student progress. But how can it be put into practice in the classroom?
Exploration, inquiry, and investigation
In Mathematical Mindsets, Jo Boaler shared her observations about what excitement looks like in the mathematics classroom: “it combines curiosity, connection making, challenge, and creativity and usually involves collaboration” and she describes tasks that all teachers can use to create this level of excitement in their classrooms (Boaler J. , 2016). In exactly the same way the examples suggested by Jennifer Wathall (Wathall, 2016) to develop the concept-based mathematics classroom, and the challenging, non-repetitive practice tasks suggested as mathematical études by Colin Foster (Foster C. , 2013) have all proved to be been incredibly successful in my own classroom.
They have provided inspiring moments, kept engagement high and prompted many opportunities for discussion. All of these approaches, backed by research and successfully trialled in the classroom have been emulated within the Pearson textbook chapters leading to the development of Explore, Investigate, Practice and Challenge example tasks; they provide additional ideas and research-backed tasks to support the inquiry-based approach and promote deep conceptual understanding of mathematics.
Let’s take an example,
At the start of a an MYP5 unit on exponential relationships I began the lesson with a simple Explore task:

The Explore was presented as an open task; we had completed a review of exponents in previous lessons but had not reviewed sequences and series. The intention was to provide an appreciation of the sheer scale of exponential growth before exploring the exponential function. The students worked in groups, collaborated on their approach, and were asked to communicate their group’s solution on whiteboards. The fun really started when they were tasked with critiquing the work of the other groups!

The engagement and excitement with the task were obvious, there was a buzz in the classroom and their answers were reasoned – some groups chose the first option so they didn’t affect their parents’ finances, as can be seen in the second photo, Figure 3b.
The lesson plan was open-ended, and some students extended the task to explore how long it would take for them to become millionaires and billionaires; this led to a lot of discussion about sequences and series, and the use of graphical methods (and the concept of equivalence) to determine the solutions. Discussions also turned to algebraic methods, and I was able to introduce the concept of a logarithm function as the inverse of an exponential function within the same Explore task. A follow up lesson could include an investigation (below), where the students can apply their understanding to a real-life application (Criterion D assessment objective).

In this class task I had not presented the students with any information, it was an “explore before being informed task” as recommended by the current research that has guided the development of the Pearson MYP series. The work of Boaler and Wathall (Boaler J. , 2016) (Boaler J. 2., 2019) (Wathall, 2016) champions the advantages of student inquiry prior to the introduction of the concepts as vital in enabling deep understanding, it is also an approach that meets the aims of both the MYP and the DP. By introducing these tasks into the MYP classroom, the IA component of the DP course is more accessible. The students are already curious about mathematics and how they can use their skills to answer the “what if?” questions that are so vital to the enjoyment of mathematics.
Development of problem-solving skills
Series Editor Ibrahim Wazir provides reasoning for the inclusion of problem-solving skill development as a core component of the mathematics classroom in his introduction to the Teacher Guides that form part of the new Pearson MYP Maths series as he describes the philosophy of the series. I will outline the approach here but recommend all mathematics teachers read his philosophy, irrespective of whether you will use the MYP series; I will most certainly be sharing it with my department.
Problem-solving seems to be accompanied by some misconceptions. It has been viewed as an aspect of the taught curriculum that takes time away from moving through the content, when it should be viewed as an integral part of developing students’ ability to think. It is also arguably the main reason for studying mathematics in the first place (Foster C. 2., 2019). I have witnessed teachers confusing a “worded problem” as an example of “problem-solving” so we must have a clear distinction between the presentation of a mathematical concept within a real-life “worded question” and a true problem-solving opportunity; this leads to the question, what is a problem?
The National Council of Teachers of Mathematics defines problem solving as “engaging in a task for which the solution method is not known in advance” (NCTM, 2000) and this connects with research supporting the exploration of concepts before they are introduced formally. This must, therefore, be applied when approaching the methods for helping students develop their own strategies for problem solving. It is not an easy task for teachers, and Colin Foster summarised the issues we find in the classroom in his ATM article (Foster C. 2., 2019). He outlined the delicate balance that teachers must find between helping too much and “killing the problem”, or “letting them struggle” where they gain nothing from the experience other than a dint to their confidence.
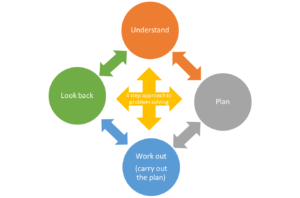
In this sense the inclusion of problem solving in the classroom must be a planned approach, it cannot be an added differentiation task, and we should heed the observation that we must scaffold the problem-solving not scaffold the problem. In this respect the adapted 4-step Polya’s approach (Polya, 2014) that is included within the series, Figure 5, is a way of scaffolding the problem-solving:
Throughout each chapter of the textbook series, the approach is demonstrated in the context of the topic being studied, and presented as a strategy for each worked solution, an example is given below, Figure 6:

In line with Colin Foster’s suggestion that Polya’s approach is “helpful when students have the necessary prior knowledge to solve the problem…” (Foster C. 2., 2019) the resources can also be used to support stand-alone problem-solving lessons when reviewing content covered previously. Returning to examples given in earlier books as problem solving tasks works well. It seems obvious that the problem-solving development goes much more smoothly when the conceptual understanding of the mathematics is already embedded. This is a vital component of a smooth transition from MYP to DP, if we try to develop problem solving skills at the start of the DP course to meet the expectations of the assessment, then the task will be much more difficult with the more complex concepts covered in class at that time, “…if the problem-solving demands are high, other demands, such as procedures and concepts, may need to be lower” (Foster C. 2., 2019).
Connections
There is a large body of research in support of teaching for conceptual understanding and developing students’ problem-solving skills and the most recent of publications connect the inquiry approach to concept exposure with a parallel development of problem-solving. When considering all the ideas, it can be summarised as encouraging students to think for themselves, to develop as inquirers, thinkers, communicators, to be open-minded, risk-takers and reflective. It is no surprise that these make up the learner profile of the IB student. It all connects; one part cannot be embraced in isolation. Teaching is a highly sophisticated dynamic system where one little tweak to a classroom practice can have a profound affect, there is no single feature that can be pinpointed as the main determinant of successful outcomes. As teachers we have an intrinsic knowledge of this, we all have stories about how one small bee managed to derail a carefully planned lesson. The same principle applies to teaching and learning, the resources used in the classroom are most effective when the teacher guiding their use is familiar with their intended purpose, and the teacher’s efforts in the classroom are intrinsically linked to the student’s level of ATL skill development. Everything is connected: the written curriculum, the taught curriculum, the development of inquiry and a growth mind-set, and the student’s ATL skills. It is serendipitous that to appreciate the interconnectedness of mathematics (Majewska, 2021) you must interconnect the learning process.
In the final blog of this series, I will discuss the role of ATL skills and assessment in the smooth transition of students from MYP to DP. I will demonstrate how the written curriculum, the taught curriculum, and the resources chosen by teachers all come together when we help students to develop the ATL skills needed to access the opportunities we can put in place.
Find out more about Pearson Mathematics for the IB Middle Years Programme on our website where you can also download chapter samples for each year group, access a sample unit plan from the Year 1 Teacher Guide, and sign up for your free trial.
Works cited
Boaler, J. (1998). Open and Closed Mathematics: Student Experiences and Understandings. Journal for Research in Mathematics Education, 29(1), 41-62.
Boaler, J. 2. (2019). Limitless Mind, Learn, and Live Without Barriers. HarperOne.
Boaler, J. (2016). Mathematical Mindsets: Unleashing Students’ Potential through Creative Math. Wiley.
Dietiker, L. R. (2019). How textbooks can promote inquiry: Using a narrative framework to investigate the design of mathematical content in a lesson. Journal for research in mathematics education, 52(3), 301-331.
Foster, C. 2. (2019). The fundamental problem with teaching problem solving. Mathematics teaching, 265, 8-10.
Foster, C. (2013). Mathematical études: Embedding opportunities for developing procedural fluency within rich mathematical contexts. International Journal of Mathematical Education in Science and Technology, 44(5), 765-774.
Sign up to receive our blog updates
Like what you read and want to receive more articles like this direct to your inbox? Subscribe to our blog and we’ll send you a fortnightly digest of the blog posts you may have missed, plus links to free resources to support your teaching and learning.