
In the second in her series of blogs, Paula Rowlands outlined how a smooth transition between MYP and DP mathematics is supported by having a seamless continuity between the components of the written curriculum and the merits of a whole school continuum plan.
In this third blog, Paula will discuss how having continuity between the programmes’ approaches to teaching and learning when following the planned units supports the MYP to DP transition.
The importance of conceptual understanding
In 1998, Jo Boaler published a research paper, ‘Open and Closed Mathematics: Student Experiences and Understandings’, presenting evidence for the benefits of a move away from a procedural approach to an inquiry and exploration-based system to develop students’ deep conceptual understanding:
‘Students who followed a traditional approach developed a procedural knowledge that was of limited use to them in unfamiliar situations. Students who learned mathematics in an open, project-based environment developed a conceptual understanding that provided them with advantages in a range of assessments and situations’.Boaler J. , 1998
The paper outlined the disadvantages observed within the procedural mathematics classroom, where the answer is important, but the understanding is not. This traditional method was contrasted with an open project-based approach and although the open approach showed disadvantages, including a reluctance on the part of the students to think, the evidence in support of a move away from traditional demonstration and repetition was clear. A concept-based approach to teaching and learning mathematics allows students to develop a deeper conceptual understanding but it should be used with a balance of procedural fluency, as described by Jennifer Wathall:
“The relationship between the facts, skills, and conceptual understandings is one that needs to be developed if we want our students to be able to apply their skills and knowledge to different contexts and to utilize higher order thinking”.Wathall, 2016
Whilst there is a need to balance efficient procedural skills and conceptual understanding, time pressures can result in opportunities for inquiry and development of problem-solving skills being relegated in favour of content coverage, particularly at the Diploma level. However, investment of time in this type of learning activity far outweighs any perceived benefits of covering content to “get an answer” with a limited understanding of how it was derived. The examples of student work shown in Figures 1a and 1b below demonstrate the consequence quite clearly.
Student A understood the concept of a logarithm having a numerical value and used their understanding to answer both the familiar and the unfamiliar questions, shown in Figure 1a.

Student B, however, was focused on using a procedure that allowed them to calculate the correct answer for the familiar question part(a) but not apply their understanding to the unfamiliar question part(b), Figure 1b.
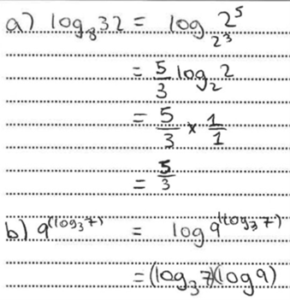
A student who takes a procedural approach to mathematics mistakenly believes that mathematics is a series of procedures to be memorised and applied in test conditions. Jankvist and Niss discuss how these misconceptions hold back a student’s progress and suggest ways in which they can be counteracted. (Jankvist, 2018). As part of the publication, they gave a list of misconceptions which identified ‘students’ conception of mathematics as a set of basically meaningless disconnected procedures that have to be memorised’ (Jankvist, 2018) and they corroborated the following misconceptions from an earlier study (Shoenfeld, 1992):
i. Mathematics problems have only one right answer.
ii. There is only one way to solve any mathematics problem.
iii. Ordinary students cannot be expected to understand mathematics; they expect to simply memorize it and apply what they have learned mechanically and without understanding.
iv. Mathematics is a solitary activity.
v. Students who have understood the mathematics they have studied will be able to solve any assigned problem in five minutes or less.
If these misconceptions carry through to DP from MYP then the effect on student grades is measurable. In the DP assessment in Figures 1a and 1b above, the misconception resulted in a lower attainment mark as the same approach in multiple questions compounded the loss of marks.
There is also a worrying misconception that mathematics is about performance (Boaler J. , 2016) when, as mathematics teachers, we know that it is about exploration, inquiry, observation, and problem-solving. It goes without saying that MYP units must be approached in such a way as to dispel these myths, to open students’ eyes to the nature of mathematics as an exploratory subject that rewards the curious, where ideas can be shared and discussed, and solutions are unearthed through persistence, not necessarily seen immediately. It is also important to disassociate progress from a perceived need to perform.
A change to a conceptual approach to mathematical tasks can open many doors for students, in particular improved access to the DP mathematics curricula. The DP Subject Guides state quite clearly, ‘conceptual understandings are key to promoting deep learning’ (IB DP AA and AI, 2019) and this is also stated clearly in the MYP Guide, ‘Concepts express understanding that students take with them into lifelong learning. They help students to develop principles, generalizations and theories. Students use conceptual understanding as they solve problems, analyse issues and evaluate decisions that can have an impact on themselves, their communities and the wider world’ (IB MYP, 2020). Therefore, a conceptual approach to teaching and learning in the MYP will smooth the transition for students into the DP. Changing a student’s approach from procedural to conceptual in the first year of the DP programme can be done. However, from experience, it does make the start of the course more challenging for the student.
Although there is sometimes a slight confusion for mathematics teachers when discussing mathematical concepts and IB concepts, in some respects they are the same. The conceptual understanding of the mathematics is framed within the ‘big picture’ concepts highlighted in the DP and MYP Guides; this helps students see how the same concepts transcend subjects.
For example, the key concept of form allows the mathematics teacher to guide students’ exploration of the way variable relationships (another key concept!) can be represented (a related concept!) in different mathematics forms (the key concept), such as function notation, mapping diagrams, and coordinate graphs. Similarly, the concept of equivalence allows students to understand the connection between solving equations algebraically and graphically. When investigated in this context students are comfortable moving between methods, using a different method to justify their solution is seen through the eyes of mathematical reasoning rather than a procedure to be followed.
In my next blog post in this series, I will explore putting an inquiry-based approach into practice in the MYP Maths classroom, and how the new Pearson Mathematics for IB Middle Years Programme series can support teachers when implementing the taught curriculum.
Find out more about Pearson Mathematics for the IB Middle Years Programme on our website where you can also download chapter samples for each year group, access a sample unit plan from the Year 1 Teacher Guide, and sign up for your free trial.
Sign up to receive our blog updates
Like what you read and want to receive more articles like this direct to your inbox? Subscribe to our blog and we’ll send you a fortnightly digest of the blog posts you may have missed, plus links to free resources to support your teaching and learning.

